DDPG: Deep Deterministic Policy Gradients
This blogpost will talk about Deep Deterministic Policy Gradients.
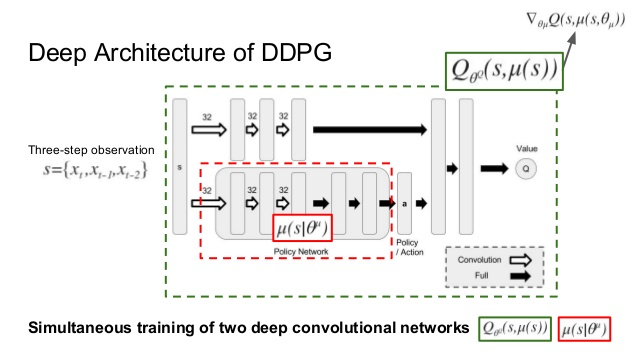
The popular DQN solves problems with high-dimensional observation spaces, it can only handle discrete and low-dimensional action spaces. Many tasks of interest, most notably physical control tasks, have continuous (real valued) and high dimensional action spaces.
To extend DQN to continuous control tasks, we need to perform an extra expensive optimization procedure in the inner loop of training(during the bellman update stage) as shown below:
\[Q(s_t,a_t) = r(s_t,a_t) + \gamma \times Q(s_{t+1},\mathbin{\color{red}{\underset{a'}{max}Q(s_{t+1},a')}})\]One may use SGD to solve this but it turns out to be quite slow. The other solutions includes sampling actions, CEM, CMA-ES etc , which often works for action dimensions upto 40. Another option is to use Easily maximizable Q Functions, where you gain computational efficiency and simplicity but loose representational power. DDPG is the third approach and most widely used out of its simplicity in implementation, and similarity to well known topics like Q Learning and Policy Gradients.
DDPG: can be interpreted in terms of Q Learning and Policy Gradients Literature. In terms of Q Learning, it tends to use a function approximator for solving the max in the Bellman Equation of Q Learning(approximate Q Learning Method).
This is achieved by learning a deterministic policy $\mu_{\theta}(s)$ using an actor neural net and updating the policy parameters by moving them in the direction of the gradient of the action-value function.
\begin{equation} \begin{aligned} \theta :=\quad& \theta\quad + \quad \alpha\times\underset{j}{\sum}\nabla_\theta Q(s_j,\mu_\theta(s)) \newline =\quad & \theta \quad + \quad \alpha\times\underset{j}{\sum}\nabla_{\mu_\theta} Q(s_j,\mu_\theta(s_j)) \times \nabla_{\theta}\mu_\theta(s_j) \newline =\quad & \theta \quad+\quad\alpha\times\underset{j}{\sum}\nabla_{a} Q(s_j,a)\times\nabla_{\theta}\mu_\theta(s_j) \end{aligned} \end{equation}
The above update rule is a special limiting case of the Policy Gradient theorem and its convergence to a locally optimal policy is proven. This is the policy gradient explanation of the algorithm and hence the name DD-Policy Gradient(For more details refer [2]).
You can find the implementation of it on a HalfCheetah Environment using OpenAI-BASELINES here.
References
- Sutton et al. 1998Policy Gradient Methods for RL with Function Approximation
- Silver et al. 2016 Deterministic Policy Gradient Algorithms
- DDPG Blog
Enjoy Reading This Article?
Here are some more articles you might like to read next: